반응형
6-1 신경망 알고리즘을 벡터화하여 한 번에 전체 샘플 사용
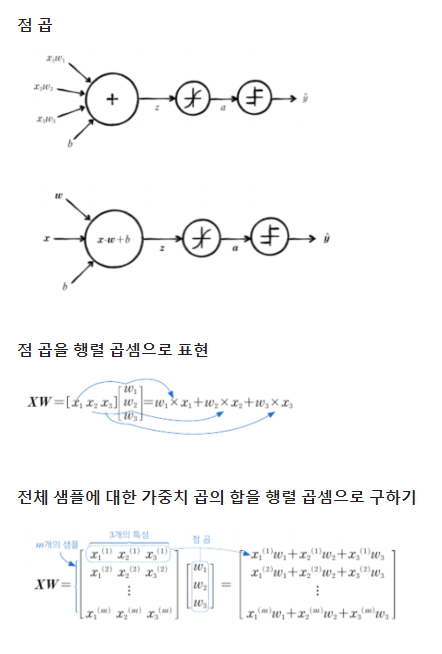
- 벡터화
벡터화(vectorization)된 연산을 사용하면 알고리즘의 성능을 높일 수 있음
- 벡터 연산과 행렬 연산
- SingleLayer 클래스에 배치 경사 하강법 적용
1. 넘파이와 맷플롯립 임포트
import numpy as np
import matplotlib.pyplot as plt
2. 위스콘신 유방암 데이터 세트를 훈련, 검증, 테스트 세트로 나누기
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
x = cancer.data
y = cancer.target
x_train_all, x_test, y_train_all, y_test = train_test_split(x, y, stratify=y, test_size=0.2, random_state=42)
x_train, x_val, y_train, y_val = train_test_split(x_train_all, y_train_all, stratify=y_train_all, test_size=0.2, random_state=42)
3. 훈련 세트와 검증 세트의 크기 확인
print(x_train.shape, x_val.shape)
##출력: (364, 30) (91, 30)
4. 정방향 계산을 행렬 곱셈으로 표현
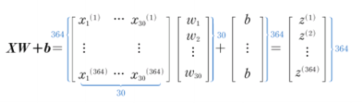

5. 그레이디언트 계산 이해

6. forpass(), backprop() 메서드에 배치 경사 하강법 적용
def forpass(self, x):
z = np.dot(x, self.w) + self.b # 선형 출력을 계산합니다.
return z
def backprop(self, x, err):
m = len(x)
w_grad = np.dot(x.T, err) / m # 가중치에 대한 그래디언트를 계산합니다.
b_grad = np.sum(err) / m # 절편에 대한 그래디언트를 계산합니다.
return w_grad, b_grad
7. fit() 메서드 수정
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1) # 타깃을 열 벡터로 바꿉니다.
y_val = y_val.reshape(-1, 1)
m = len(x) # 샘플 개수를 저장합니다.
self.w = np.ones((x.shape[1], 1)) # 가중치를 초기화합니다.
self.b = 0 # 절편을 초기화합니다.
self.w_history.append(self.w.copy()) # 가중치를 기록합니다.
# epochs만큼 반복합니다.
for i in range(epochs):
z = self.forpass(x) # 정방향 계산을 수행합니다.
a = self.activation(z) # 활성화 함수를 적용합니다.
err = -(y - a) # 오차를 계산합니다.
# 오차를 역전파하여 그래디언트를 계산합니다.
w_grad, b_grad = self.backprop(x, err)
# 그래디언트에 페널티 항의 미분 값을 더합니다.
w_grad += (self.l1 * np.sign(self.w) + self.l2 * self.w) / m
# 가중치와 절편을 업데이트합니다.
self.w -= self.lr * w_grad
self.b -= self.lr * b_grad
# 가중치를 기록합니다.
self.w_history.append(self.w.copy())
# 안전한 로그 계산을 위해 클리핑합니다.
a = np.clip(a, 1e-10, 1-1e-10)
# 로그 손실과 규제 손실을 더하여 리스트에 추가합니다.
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / m)
# 검증 세트에 대한 손실을 계산합니다.
self.update_val_loss(x_val, y_val)
8. 나머지 메서드 수정
def predict(self, x):
z = self.forpass(x) # 정방향 계산을 수행합니다.
return z > 0 # 스텝 함수를 적용합니다.
def update_val_loss(self, x_val, y_val):
z = self.forpass(x_val) # 정방향 계산을 수행합니다.
a = self.activation(z) # 활성화 함수를 적용합니다.
a = np.clip(a, 1e-10, 1-1e-10) # 출력 값을 클리핑합니다.
# 로그 손실과 규제 손실을 더하여 리스트에 추가합니다.
val_loss = np.sum(-(y_val*np.log(a) + (1-y_val)*np.log(1-a)))
self.val_losses.append((val_loss + self.reg_loss()) / len(y_val))
9. 훈련 데이터 표준화 전처리
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(x_train)
x_train_scaled = scaler.transform(x_train)
x_val_scaled = scaler.transform(x_val)
10. 데이터를 SingleLayer 클래스 객체에 전달하여 배치 경사 하강법 적용
single_layer = SingleLayer(l2=0.01)
single_layer.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val, epochs=10000)
single_layer.score(x_val_scaled, y_val)
##출력: 0.978021978021978
11. 검증 세트로 성능 측정, 그래프로 비교
plt.ylim(0, 0.3)
plt.plot(single_layer.losses)
plt.plot(single_layer.val_losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'])
plt.show()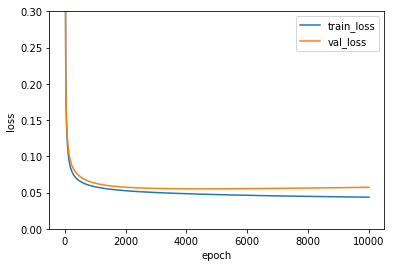
12. 가중치의 변화 그래프로 나타내기
w2 = []
w3 = []
for w in single_layer.w_history:
w2.append(w[2])
w3.append(w[3])
plt.plot(w2, w3)
plt.plot(w2[-1], w3[-1], 'ro')
plt.xlabel('w[2]')
plt.ylabel('w[3]')
plt.show()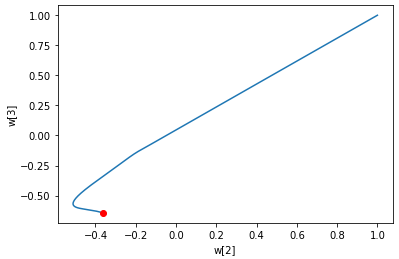
※ SingleLayer 전체 클래스 코드
class SingleLayer:
def __init__(self, learning_rate=0.1, l1=0, l2=0):
self.w = None # 가중치
self.b = None # 절편
self.losses = [] # 훈련 손실
self.val_losses = [] # 검증 손실
self.w_history = [] # 가중치 기록
self.lr = learning_rate # 학습률
self.l1 = l1 # L1 손실 하이퍼파라미터
self.l2 = l2 # L2 손실 하이퍼파라미터
def forpass(self, x):
z = np.dot(x, self.w) + self.b # 선형 출력을 계산합니다.
return z
def backprop(self, x, err):
m = len(x)
w_grad = np.dot(x.T, err) / m # 가중치에 대한 그래디언트를 계산합니다.
b_grad = np.sum(err) / m # 절편에 대한 그래디언트를 계산합니다.
return w_grad, b_grad
def activation(self, z):
z = np.clip(z, -100, None) # 안전한 np.exp() 계산을 위해
a = 1 / (1 + np.exp(-z)) # 시그모이드 계산
return a
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1) # 타깃을 열 벡터로 바꿉니다.
y_val = y_val.reshape(-1, 1)
m = len(x) # 샘플 개수를 저장합니다.
self.w = np.ones((x.shape[1], 1)) # 가중치를 초기화합니다.
self.b = 0 # 절편을 초기화합니다.
self.w_history.append(self.w.copy()) # 가중치를 기록합니다.
# epochs만큼 반복합니다.
for i in range(epochs):
z = self.forpass(x) # 정방향 계산을 수행합니다.
a = self.activation(z) # 활성화 함수를 적용합니다.
err = -(y - a) # 오차를 계산합니다.
# 오차를 역전파하여 그래디언트를 계산합니다.
w_grad, b_grad = self.backprop(x, err)
# 그래디언트에 페널티 항의 미분 값을 더합니다.
w_grad += (self.l1 * np.sign(self.w) + self.l2 * self.w) / m
# 가중치와 절편을 업데이트합니다.
self.w -= self.lr * w_grad
self.b -= self.lr * b_grad
# 가중치를 기록합니다.
self.w_history.append(self.w.copy())
# 안전한 로그 계산을 위해 클리핑합니다.
a = np.clip(a, 1e-10, 1-1e-10)
# 로그 손실과 규제 손실을 더하여 리스트에 추가합니다.
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / m)
# 검증 세트에 대한 손실을 계산합니다.
self.update_val_loss(x_val, y_val)
def predict(self, x):
z = self.forpass(x) # 정방향 계산을 수행합니다.
return z > 0 # 스텝 함수를 적용합니다.
def score(self, x, y):
# 예측과 타깃 열 벡터를 비교하여 True의 비율을 반환합니다.
return np.mean(self.predict(x) == y.reshape(-1, 1))
def reg_loss(self):
# 가중치에 규제를 적용합니다.
return self.l1 * np.sum(np.abs(self.w)) + self.l2 / 2 * np.sum(self.w**2)
def update_val_loss(self, x_val, y_val):
z = self.forpass(x_val) # 정방향 계산을 수행합니다.
a = self.activation(z) # 활성화 함수를 적용합니다.
a = np.clip(a, 1e-10, 1-1e-10) # 출력 값을 클리핑합니다.
# 로그 손실과 규제 손실을 더하여 리스트에 추가합니다.
val_loss = np.sum(-(y_val*np.log(a) + (1-y_val)*np.log(1-a)))
self.val_losses.append((val_loss + self.reg_loss()) / len(y_val))
※ 해당 내용은 <Do it! 딥러닝 입문>의 내용을 토대로 학습하며 정리한 내용입니다.
반응형
'딥러닝 학습' 카테고리의 다른 글
| 6장 2개의 층을 연결 - 다층 신경망 (3) (0) | 2023.03.11 |
|---|---|
| 6장 2개의 층을 연결 - 다층 신경망 (2) (0) | 2023.03.10 |
| 5장 훈련 노하우 배우기 (3) (0) | 2023.03.08 |
| 5장 훈련 노하우 배우기 (2) (0) | 2023.03.07 |
| 5장 훈련 노하우 배우기 (1) (0) | 2023.03.06 |



