반응형
- 2개의 층을 가진 신경망 구현
1. SingleLayer 클래스를 상속한 DualLayer 클래스 만들기
class DualLayer(SingleLayer):
def __init__(self, units=10, learning_rate=0.1, l1=0, l2=0):
self.units = units # 은닉층의 뉴런 개수
self.w1 = None # 은닉층의 가중치
self.b1 = None # 은닉층의 절편
self.w2 = None # 출력층의 가중치
self.b2 = None # 출력층의 절편
self.a1 = None # 은닉층의 활성화 출력
self.losses = [] # 훈련 손실
self.val_losses = [] # 검증 손실
self.lr = learning_rate # 학습률
self.l1 = l1 # L1 손실 하이퍼파라미터
self.l2 = l2 # L2 손실 하이퍼파라미터
2. forpass() 메서드 수정하기
def forpass(self, x):
z1 = np.dot(x, self.w1) + self.b1 # 첫 번째 층의 선형 식을 계산합니다
self.a1 = self.activation(z1) # 활성화 함수를 적용합니다
z2 = np.dot(self.a1, self.w2) + self.b2 # 두 번째 층의 선형 식을 계산합니다.
return z2
3. backprop() 메서드 수정하기
def backprop(self, x, err):
m = len(x) # 샘플 개수
# 출력층의 가중치와 절편에 대한 그래디언트를 계산합니다.
w2_grad = np.dot(self.a1.T, err) / m
b2_grad = np.sum(err) / m
# 시그모이드 함수까지 그래디언트를 계산합니다.
err_to_hidden = np.dot(err, self.w2.T) * self.a1 * (1 - self.a1)
# 은닉층의 가중치와 절편에 대한 그래디언트를 계산합니다.
w1_grad = np.dot(x.T, err_to_hidden) / m
b1_grad = np.sum(err_to_hidden, axis=0) / m
return w1_grad, b1_grad, w2_grad, b2_grad
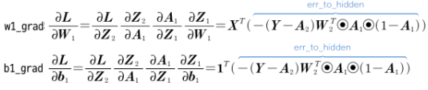
4. fit() 메서드 수정
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1) # 타깃을 열 벡터로 바꿉니다.
y_val = y_val.reshape(-1, 1)
m = len(x) # 샘플 개수를 저장합니다.
self.init_weights(x.shape[1]) # 은닉층과 출력층의 가중치를 초기화합니다.
# epochs만큼 반복합니다.
for i in range(epochs):
a = self.training(x, y, m)
# 안전한 로그 계산을 위해 클리핑합니다.
a = np.clip(a, 1e-10, 1-1e-10)
# 로그 손실과 규제 손실을 더하여 리스트에 추가합니다.
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / m)
# 검증 세트에 대한 손실을 계산합니다.
self.update_val_loss(x_val, y_val)
5. fit() 메서드에 있던 가중치 초기화 부분 init_weights() 메서드로 분리
def init_weights(self, n_features):
self.w1 = np.ones((n_features, self.units)) # (특성 개수, 은닉층의 크기)
self.b1 = np.zeros(self.units) # 은닉층의 크기
self.w2 = np.ones((self.units, 1)) # (은닉층의 크기, 1)
self.b2 = 0
6. fit() 메서드의 for문 안에 있는 코드 중 일부를 training() 메서드로 분리
def training(self, x, y, m):
z = self.forpass(x) # 정방향 계산을 수행합니다.
a = self.activation(z) # 활성화 함수를 적용합니다.
err = -(y - a) # 오차를 계산합니다.
# 오차를 역전파하여 그래디언트를 계산합니다.
w1_grad, b1_grad, w2_grad, b2_grad = self.backprop(x, err)
# 그래디언트에 페널티 항의 미분 값을 더합니다
w1_grad += (self.l1 * np.sign(self.w1) + self.l2 * self.w1) / m
w2_grad += (self.l1 * np.sign(self.w2) + self.l2 * self.w2) / m
# 은닉층의 가중치와 절편을 업데이트합니다.
self.w1 -= self.lr * w1_grad
self.b1 -= self.lr * b1_grad
# 출력층의 가중치와 절편을 업데이트합니다.
self.w2 -= self.lr * w2_grad
self.b2 -= self.lr * b2_grad
return a
7. reg_loss() 메서드 수정
def reg_loss(self):
# 은닉층과 출력층의 가중치에 규제를 적용합니다.
return self.l1 * (np.sum(np.abs(self.w1)) + np.sum(np.abs(self.w2))) + self.l2 / 2 * (np.sum(self.w1**2) + np.sum(self.w2**2))
※ DualLayer 클래스 코드
class DualLayer(SingleLayer):
def __init__(self, units=10, learning_rate=0.1, l1=0, l2=0):
self.units = units # 은닉층의 뉴런 개수
self.w1 = None # 은닉층의 가중치
self.b1 = None # 은닉층의 절편
self.w2 = None # 출력층의 가중치
self.b2 = None # 출력층의 절편
self.a1 = None # 은닉층의 활성화 출력
self.losses = [] # 훈련 손실
self.val_losses = [] # 검증 손실
self.lr = learning_rate # 학습률
self.l1 = l1 # L1 손실 하이퍼파라미터
self.l2 = l2 # L2 손실 하이퍼파라미터
def forpass(self, x):
z1 = np.dot(x, self.w1) + self.b1 # 첫 번째 층의 선형 식을 계산합니다
self.a1 = self.activation(z1) # 활성화 함수를 적용합니다
z2 = np.dot(self.a1, self.w2) + self.b2 # 두 번째 층의 선형 식을 계산합니다.
return z2
def backprop(self, x, err):
m = len(x) # 샘플 개수
# 출력층의 가중치와 절편에 대한 그래디언트를 계산합니다.
w2_grad = np.dot(self.a1.T, err) / m
b2_grad = np.sum(err) / m
# 시그모이드 함수까지 그래디언트를 계산합니다.
err_to_hidden = np.dot(err, self.w2.T) * self.a1 * (1 - self.a1)
# 은닉층의 가중치와 절편에 대한 그래디언트를 계산합니다.
w1_grad = np.dot(x.T, err_to_hidden) / m
b1_grad = np.sum(err_to_hidden, axis=0) / m
return w1_grad, b1_grad, w2_grad, b2_grad
def init_weights(self, n_features):
self.w1 = np.ones((n_features, self.units)) # (특성 개수, 은닉층의 크기)
self.b1 = np.zeros(self.units) # 은닉층의 크기
self.w2 = np.ones((self.units, 1)) # (은닉층의 크기, 1)
self.b2 = 0
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1) # 타깃을 열 벡터로 바꿉니다.
y_val = y_val.reshape(-1, 1)
m = len(x) # 샘플 개수를 저장합니다.
self.init_weights(x.shape[1]) # 은닉층과 출력층의 가중치를 초기화합니다.
# epochs만큼 반복합니다.
for i in range(epochs):
a = self.training(x, y, m)
# 안전한 로그 계산을 위해 클리핑합니다.
a = np.clip(a, 1e-10, 1-1e-10)
# 로그 손실과 규제 손실을 더하여 리스트에 추가합니다.
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / m)
# 검증 세트에 대한 손실을 계산합니다.
self.update_val_loss(x_val, y_val)
def training(self, x, y, m):
z = self.forpass(x) # 정방향 계산을 수행합니다.
a = self.activation(z) # 활성화 함수를 적용합니다.
err = -(y - a) # 오차를 계산합니다.
# 오차를 역전파하여 그래디언트를 계산합니다.
w1_grad, b1_grad, w2_grad, b2_grad = self.backprop(x, err)
# 그래디언트에 페널티 항의 미분 값을 더합니다
w1_grad += (self.l1 * np.sign(self.w1) + self.l2 * self.w1) / m
w2_grad += (self.l1 * np.sign(self.w2) + self.l2 * self.w2) / m
# 은닉층의 가중치와 절편을 업데이트합니다.
self.w1 -= self.lr * w1_grad
self.b1 -= self.lr * b1_grad
# 출력층의 가중치와 절편을 업데이트합니다.
self.w2 -= self.lr * w2_grad
self.b2 -= self.lr * b2_grad
return a
def reg_loss(self):
# 은닉층과 출력층의 가중치에 규제를 적용합니다.
return self.l1 * (np.sum(np.abs(self.w1)) + np.sum(np.abs(self.w2))) + \
self.l2 / 2 * (np.sum(self.w1**2) + np.sum(self.w2**2))반응형
- 모델 훈련하기
1. 다층 신경망 모델 훈련하고 평가
dual_layer = DualLayer(l2=0.01)
dual_layer.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val, epochs=20000)
dual_layer.score(x_val_scaled, y_val)
##출력: 0.978021978021978
2. 훈련 손실과 검증 손실 그래프 분석
plt.ylim(0, 0.3)
plt.plot(dual_layer.losses)
plt.plot(dual_layer.val_losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'])
plt.show()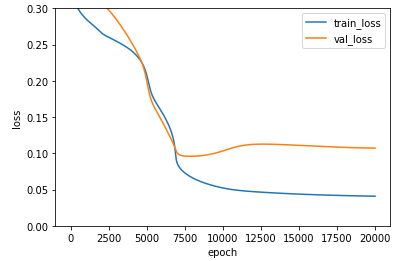
- 가중치 초기화 개선
1. 가중치 초기화를 위한 init_weights() 메서드 수정
class RandomInitNetwork(DualLayer):
def init_weights(self, n_features):
np.random.seed(42)
self.w1 = np.random.normal(0, 1, (n_features, self.units)) # (특성 개수, 은닉층의 크기)
self.b1 = np.zeros(self.units) # 은닉층의 크기
self.w2 = np.random.normal(0, 1, (self.units, 1)) # (은닉층의 크기, 1)
self.b2 = 0
2. RandomInitNetwork 클래스 객체를 다시 만들고 모델 훈련
random_init_net = RandomInitNetwork(l2=0.01)
random_init_net.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val, epochs=500)
plt.plot(random_init_net.losses)
plt.plot(random_init_net.val_losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'])
plt.show()
※ 해당 내용은 <Do it! 딥러닝 입문>의 내용을 토대로 학습하며 정리한 내용입니다.
반응형
'딥러닝 학습' 카테고리의 다른 글
| 7장 여러개를 분류 - 다중 분류 (1) (0) | 2023.03.13 |
|---|---|
| 6장 2개의 층을 연결 - 다층 신경망 (4) (0) | 2023.03.12 |
| 6장 2개의 층을 연결 - 다층 신경망 (2) (0) | 2023.03.10 |
| 6장 2개의 층을 연결 - 다층 신경망 (1) (0) | 2023.03.09 |
| 5장 훈련 노하우 배우기 (3) (0) | 2023.03.08 |



